筆者の勤務先であるモノグサ社では、「未体験への挑戦」という行動指針を掲げています。
そして、「未体験への挑戦」は、今年のアドベントカレンダーの執筆テーマでもあります。
さて、Atom フィードをフォローしてくれている方はご存知だと思いますが、今年の 1 月に当ブログでは「あるスタートアップのリファラル事情」という記事を掲載しました。年始に帰省した主人公が、幼馴染に呼び出されてファミレスでリファラルを受ける話です。
このスタートアップというのは、モノグサ社のことではなく、物語の中に登場する架空の会社なのですが、しかしモノグサ社ともいくつかの共通点があるようです。
一つはスタートアップであること。会社の規模としては、物語の中の会社では社員が 8 人しかいないのに対して、モノグサ社では 200 人近いので、ずいぶん違いがありますが、いずれもスタートアップであることは変わりません。
もう一つは、リファラル採用に力を入れていること。つまり、採用のルートとして求人サイトなどよりも、既存社員の紹介による人材募集を重視するということです。もっとも、物語の中の会社のように「リファラルのみ」というのは極端ですし（しかし、その人数の会社では割とあることだとも思います）、モノグサ社では私も含めて求人サイトから来た人も多いですが、それでもリファラルは主要なルートの一つです。
そしてもう一つは、挑戦を支援する姿勢。主人公の友人は、自分だけでなく他人や会社の成長のために、自分からアクションを取っている行動力のある人物として描かれています。それは、モノグサ社でも推奨されていることです。
ただ、問題を掲載しておきながら、解説編を掲載していなかったので、ここで記しておくことにしましょう。
物語のあらすじ
元記事はちょっとした物語形式になっていて長いので、問題の部分だけを再掲しておきます。主人公が、スタートアップのリファラルに関心を示したところからです。
友人が紹介した求人について、その熱量に押されたあなたは、「ちょっと興味はある」と答えました。
すると、友人は嬉しそうに一枚のメモを広げます。
「ありがとう。その場合はね、開発部長からメッセージを預かってるんだ」
当社開発職へのエントリーありがとうございます。
当社には、営業職 3 名と開発職 5 名のあわせて 8 名の社員がいます。このうち、営業職である創業者 1 名を除き、他の 7 名は、それぞれ当時の既存社員 1 名を推薦人として、推薦人からの推薦によって採用されました。
その際、当社では、推薦人について、入社者と異なる職種（営業職→開発職、開発職→営業職）でなければならないという条件を課しています。また、創業以来、退職した者はいません。
これらの情報にもとづいて、当社の人物相関図を想像するとき、あり得る人物相関図は何通りあるでしょうか？
ただし、人物相関図とは、紙面上に社員の顔写真を配置し、「推薦した→推薦された」という関係を表すために、推薦した社員を起点、推薦された社員を終点とする矢印を描き込んだ図のことをいいます。また、人物相関図を数える際には、写真の配置や矢印の描き方が異なっても、全く同じ「推薦した→推薦された」関係を表している人物相関図は、まとめて 1 通りとして数えます。
読み終わると、友人はメッセージの紙をテーブルに置いて、あなたが読みやすい向きに直しました。
余白がずいぶん大きいのは、計算用紙ということなのでしょう。
「飲み物取ってくるね。何がいい？」
あなたは「アイスコーヒー」と告げて、ドリンクバーに向かう友人を見送ると、バッグからボールペンを取り出し、考察を始めることにしました。
アイスコーヒーは、ドリンクバーの中では時間がかかりそうな飲み物です。もし混雑していれば、3 分くらいは時間が稼げるかもしれません。主人公は、とっさに機転を利かせることができる人物なのですね。
それでは、その 3 分間で、主人公はどんなことを考えるのでしょうか。
なお、問題文がやや不明瞭ですが、設定として「誰が創業者であるかは知っているが、他の社員の入社順は知らない」という前提で考えるものと補足させてください。
数学の言葉に置き換える
本問は、「何通りありますか」という問題です。このようなものは、数え上げの問題とよばれていますね。とくに本問では、問題文で示された「人物相関図」というものが何通りあり得るかを考えています。
数え上げの問題なので、順列や組合せなどといった、数学の手法を使って考えていくのがよさそうです。そのためには、日常の日本語で書かれた文章題のままではなく、数学の用語を使った形に読み替えることが第一歩です。
問題文に書かれていることを、一つ一つ、数学の言葉に置き換えていきましょう。
「人物相関図」
まず、本問の関心の対象である「人物相関図」を数学的な対象としてとらえなければなりません。離散グラフを知っている人なら、このようなものは直ちに、離散グラフを使って表現したくなるでしょう。
問題文によると、写真の配置や矢印の描き方は考慮せず、「どれとどれがつながっているか」だけを考慮するといいます。これは、まさに離散グラフの特徴に他ならないからです。
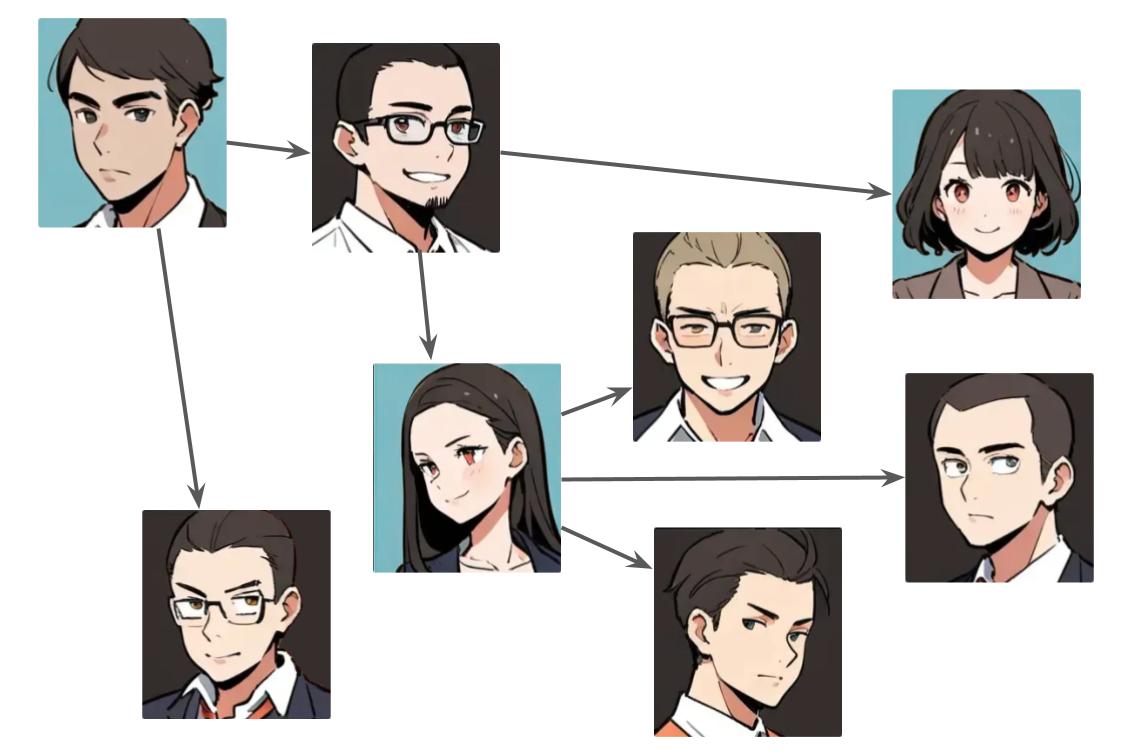
具体的には、「社員の顔写真」をグラフの頂点とし、それを結ぶ「矢印」をグラフの辺とすればよさそうです。
有向グラフと無向グラフ
ところで、一つ気になることがあります。
離散グラフには「有向グラフ」と「無向グラフ」がありますね。いずれも、頂点（ノード）を辺（エッジ）でつないだものであることは同じですが、有向グラフでは辺の始点と終点を区別するのに対し、無向グラフでは始点と終点を区別しないという違いがあります。
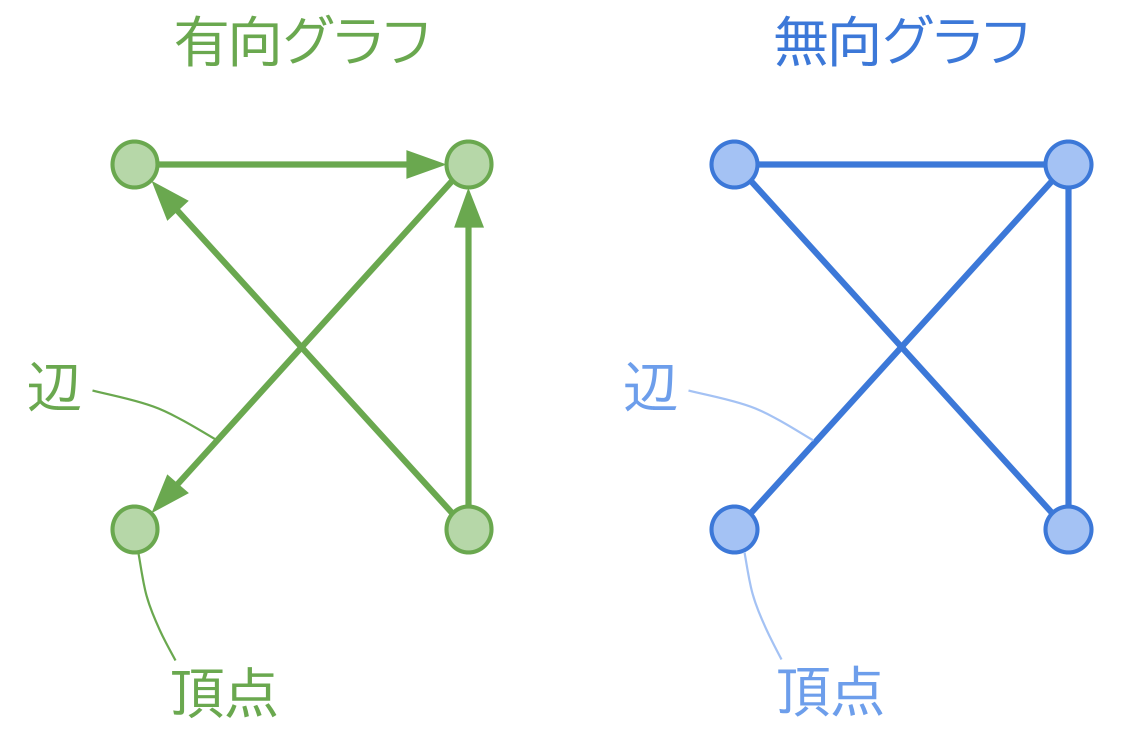
本問では、どちらを使うのが良いでしょうか？
おそらく、問題文を素直に読めば、「有向グラフを使う」という発想になりそうです。実際、問題文には「推薦した社員を起点、推薦された社員を終点とする矢印を描き込んだ図」とあるので、これをグラフで表現するなら、有向グラフとするのが自然でしょう。
しかし、実は始点と終点の違いを無視して、無向グラフとして表すのがうまいのです。このことについては、あとで説明しましょう。
頂点がもつ情報
他にも条件がありますね。問題文では、社員について「営業職」と「開発職」という区分があり、その区分によって、矢印で結んでよいかどうかが制限を受けています。
このような区分は、グラフの言葉でいえば、頂点に「色」があるということです。そして、矢印で結んでよいかどうかの制限は、グラフでは「辺の両端が同じ色であってはならない」という条件で表すことができます。
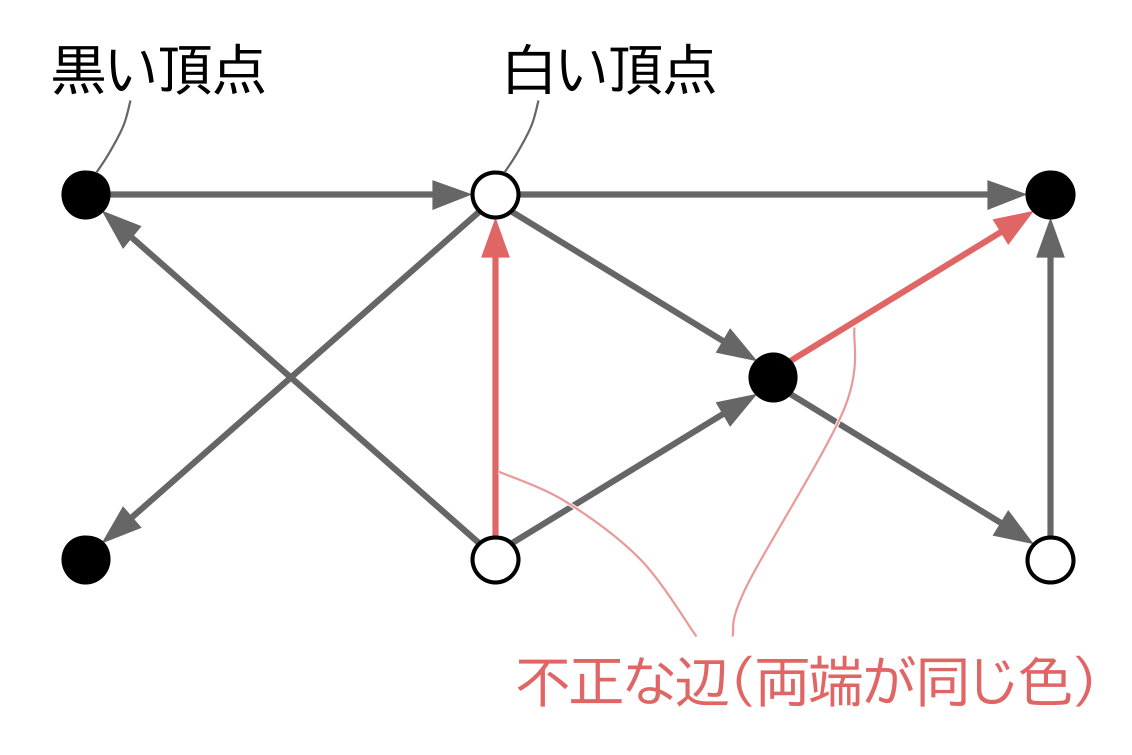
また、これらの頂点が「人」（あるいは、その写真）を表していることにも留意をしなければなりません。数え上げの問題では、慣習として、「玉」や「カード」などの物品は互いに区別をしないのに対し、「人」は一つ一つ区別をするというのが暗黙の了解です。
このことは、グラフの言葉でいえば、頂点に「番号」あるいは「名前」がついているということができます。
問題文によれば、「営業職」の社員が 3 人と、「開発職」の社員が 5 人いるということですね。
これをグラフの言葉で表すと、たとえば以下のようになるでしょう。
- 3 つの白い頂点があり，名前は A1, A2, A3
- 5 つの黒い頂点があり，名前は B1, B2, B3, B4, B5
- 辺の両端が同じ色であってはならない
なお、この 3 つめの条件には、典型的な読み替えがあるのですが、それは後で説明します。
条件をもれなく読み替える
問題文で、まだ数学の言葉に読み替えていない条件はどこでしょうか？
すべての社員がつながる
まだ読み替えていないのは、「営業職である創業者 1 名を除き、他の 7 名は、それぞれ当時の既存社員 1 名を推薦人として、推薦人からの推薦によって採用されました。」という部分です。
有向グラフでいえば、特定の白い頂点 A1 を根とした根付き木であるということを意味しています。ループや合流、逆流、離れた部分がないということです。
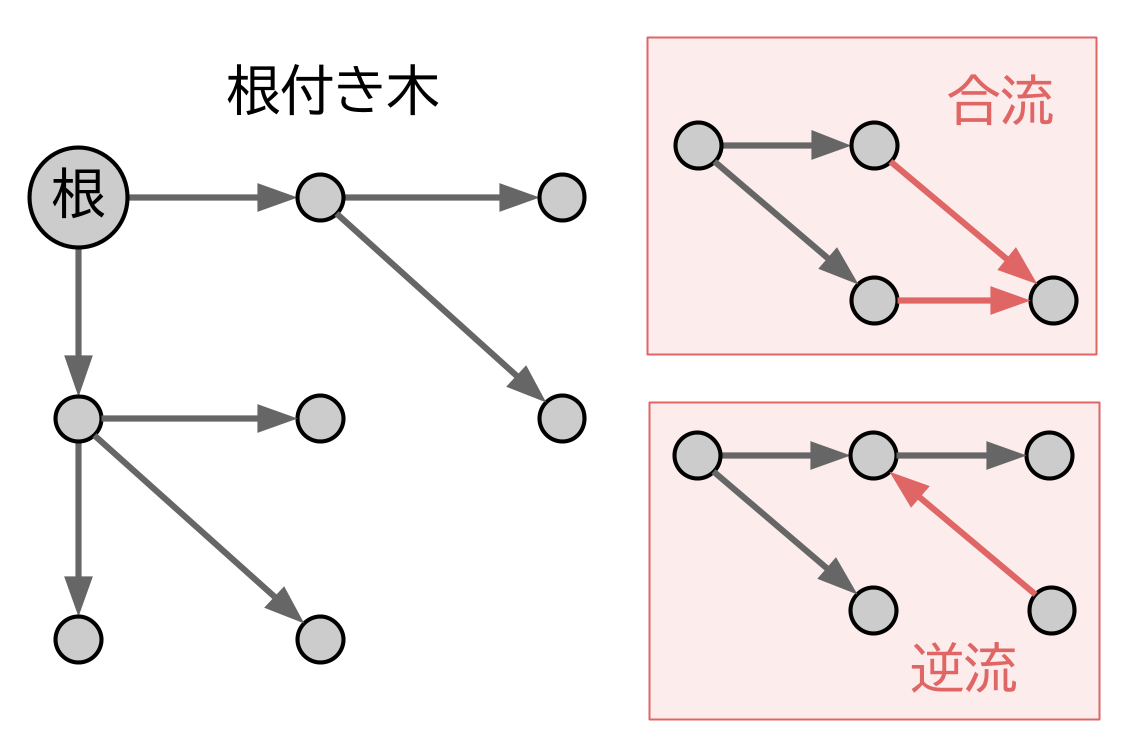
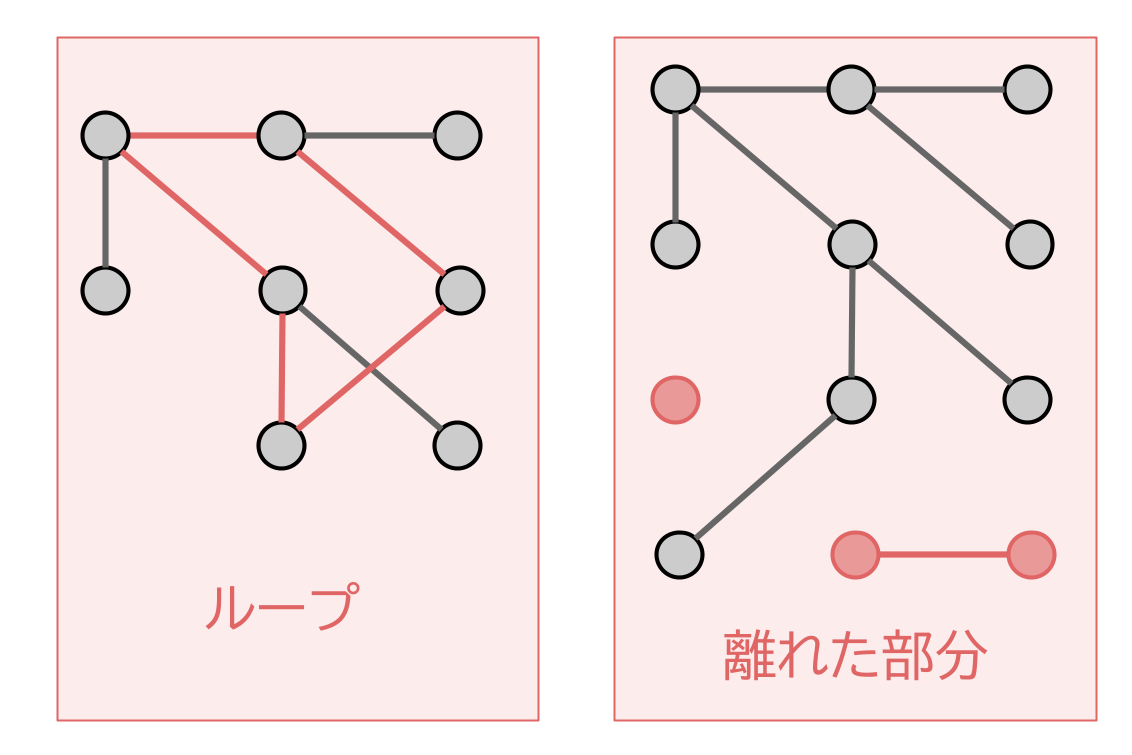
では、無向グラフでいえばどうでしょうか？
このときは、合流とか逆流といった概念はないので、単に「木である」という一言で表すことができます。ループがなく、離れた部分もないということですね。
そして、ここで「無向グラフで考えてよいのか」という話に戻りましょう。
本問は、有向グラフで考えれば、「A1 を根とする根付き木」が何通りあるかを数える問題です。これを、無向グラフで考えて、単に「木」が何通りあるかを数えることにしてしまおうというのですね。
それを大丈夫と言うためには、有向グラフの「A1 を根とする根付き木」と、無向グラフの「木」が 1 対 1 に対応づけられることを示す必要があります。
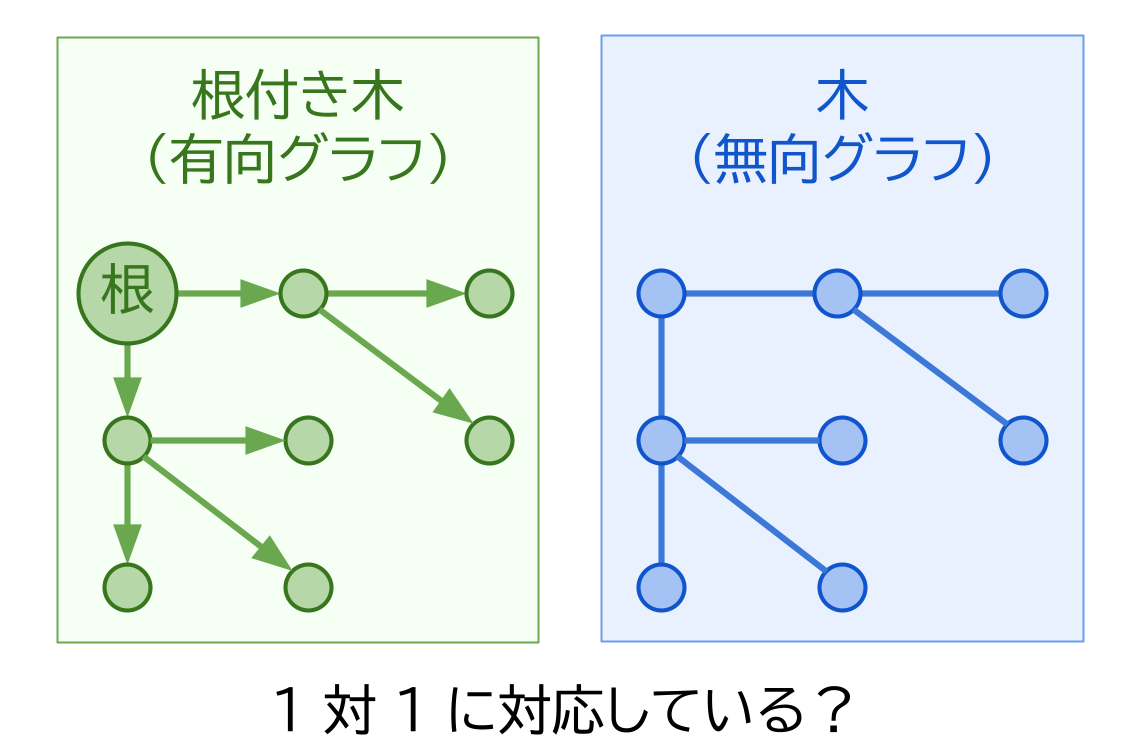
まず、有向グラフの根付き木を、無向グラフの木に対応させることは、自明に可能です。単に、根という概念を忘れ、辺の始点と終点も忘れてしまえばよいですね。
逆に、無向グラフの木から、有向グラフの根付き木を得ることもできます。各辺について、両端のうち A1 に近いほうを始点とし、A1 から遠いほうを終点とすればよいだけです。
こういうわけで、本問は有向グラフではなく、無向グラフで考えることができます。これにより、合流や逆流といった面倒なことを考えなくてすむようになるわけです。
辺の両端の色が異なる
先ほど後回しにした、「辺の両端が同じ色であってはならない」という条件の扱い方を説明しましょう。
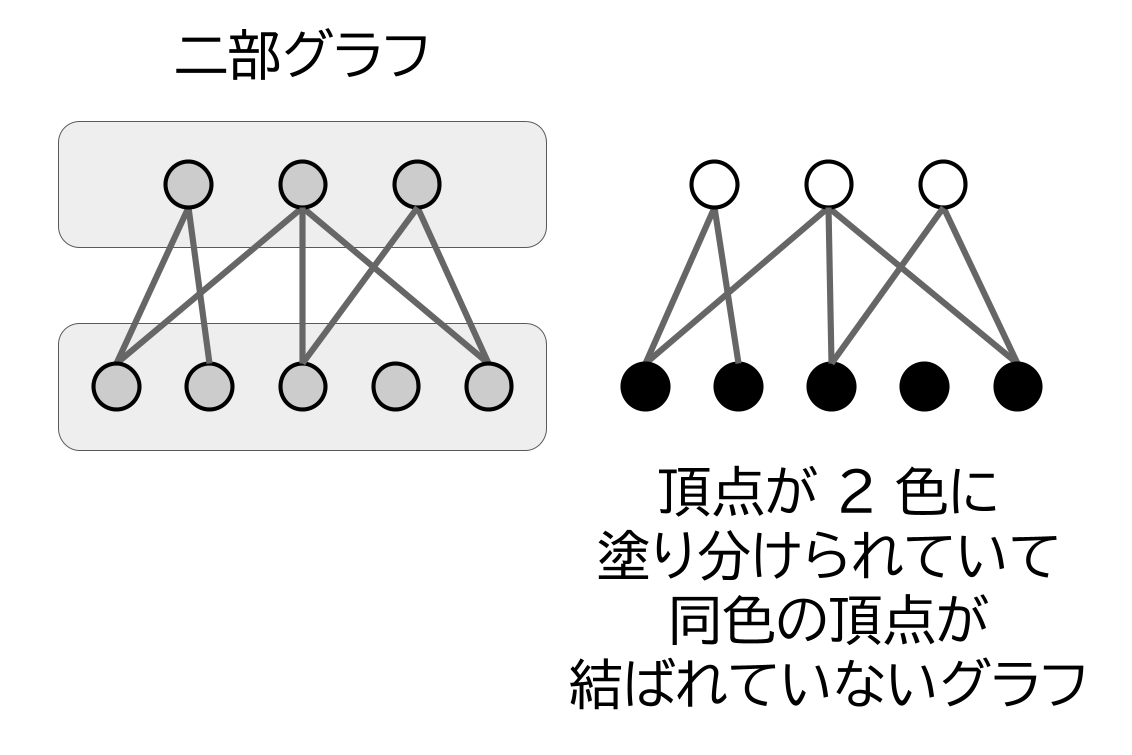
端的に言うと、これは「二部グラフである」という一言でまとめるのが定石です。
二部グラフというと、「頂点が 2 つの集合に分かれていて、それらの間に辺が張られている」というイメージをもつことが多いかもしれません。
しかし、2 つの集合を「色」とよぶことにすれば、これは「頂点が 2 色に塗り分けてあって、異なる色の頂点を結ぶ辺が張られている」という状況を言い換えたにすぎないわけです。
さあ、結論にせまってきました。ここまでをまとめると、問題はこのようになります。
1 つの頂点集合が { A1, A2, A3 } であり、もう 1 つの頂点集合が { B1, B2, B3, B4, B5 } である二部グラフを考えるとき、木であるものは何通りありますか？
ここで、ややあいまいな言い方をしていますが、木に含まれていない頂点が残っているものは不可というのが、上の問題文の意図です。
すべての頂点を通る木
ここまでは、まず頂点の集合を考えて、初めは辺がない状態から、辺を増やすことで木をつくるというイメージを描いてきました。
しかし、このような場面では、逆転の発想で、「初めに、あり得るすべての辺を描いておき、不要な辺を消して木にする」という表現の仕方をするのが定石です。
この見方をすれば、問題は「完全二部グラフの全域部分木」というテーマだったことが分かります。問題文は以下のようになります。
完全二部グラフ K3,5 の全域部分木はいくつあるか。
なお、K3,5 とは、2 つの集合に分けた頂点の個数が 3 個と 5 個である完全二部グラフのことです。
公式にあてはめて計算する
ここまで簡略化されれば、あとはどうにかなるでしょう。
以下の公式が知られています。
完全二部グラフ Ka,b がもつ全域部分木は ab−1⋅ba−1 通りである。
35−1⋅53−1 を計算して、答えは 2025 となります。
物語の結末
さて、主人公は、アイスコーヒーが出来上がるまでの 3 分間でここまでの考察ができたのでしょうか。
問題を読み替えて簡略化することができたとしても、公式を知らなければ、3 分で答えを出すのは厳しいかもしれません。（この公式の導出は、かなり込み入った考察が必要であり難しいです。）
しかし、パソコンを使ってよければ、ネット検索ですぐにこの式を見つけることはできるでしょう。筆者も、今まで知らなかったのですが、この記事の執筆に際して OEIS や Wikipedia を見たことなどによって最近知りました。
もっとも…。
手早く答えを出してしまうことが、本当に最適であるかどうかは、筆者にはわかりません。
久しぶりに幼馴染と会ったのですから、積もる話もあるでしょう。パソコンを使って、処理に 1 時間くらいかかる全探索のプログラムを書き、答えが出るのを待ちながら、ドリンクバーのコーヒーで時間をつぶすのが最適という可能性もありそうです。
